 | |||||||||
 | |||||||||
|
|
| Introduction | |||||||||
Maximilian Schuler, later a professor of dynamics at Göttingen, developed the gyroscopic ship's compass in the early 1920s and was the first to show that the error due to sideways acceleration of the ship would disappear if the compass could be tuned to a period of 84 minutes. This case presents the development of this concept starting from the single particle pendulum, the physical pendulum, and the gyro pendulum. In addition, it is shown that a number of other phenomena are subject to the same 84 minute period. A stone falling along a diameter through the center of the earth takes 84 minutes to return to its original position, assuming uniform density of the earth. The same period occurs for a body moving along a frictionless "horizontal" track, also for a body moving without friction in a straight tunnel connecting any two points on the surface of the earth, and finally for a satellite going around the earth in a low orbit. It is shown that the same period occurs for a "roof top" satellite around any other celestial body having the same density as the earth. The most important engineering application of the 84 minute pendulum is the inertial guidance system for spacecraft, missiles, airplanes, and ships. The case illustrates the effect of initial guidance platform misalignment upon the guidance error of an inertial system. | |||||||||
| Theory | |||||||||
Around the year 1920, the gyroscopic ship's compass was developed. This is a marvelous device which senses two things: the direction of the gravitational vertical and the once per 24 hour rotation of the earth about its axis. From these two inputs the compass automatically points horizontal and North and it has the astounding property of being self correcting: if the compass is disturbed and started in a position considerably different from the horizontal and North, it will slowly drift back to the desired correct position. When the first compasses were built and places in service it was found that they became completely useless on a rolling ship proceeding in a NE-SW direction. This effect was called the "intercardinal rolling error"; 'cardinal' meaning the two principal compass directions NS or EW and 'intercardinal' being between those. After exhaustive research the effect was found to be due to the sidewise accelerations of the compass caused by the rolling motion of the ship. The phenomenon was very complicated and a good practical solution was found in the 1920s by Max Schuler, the developer of the device, and later professor of dynamics at the famous University of Göttingen in Germany. On (complicated) theoretical grounds he deduced that the error would disappear if the compass was tuned to a natural period of 84 minutes. Subsequent compasses built to this specification operated satisfactorily on rolling ships on an "intercardinal" course. The term "Schuler tuning" for the compass came into general use then. Since the physical and mathematical explanation of the effect as well as the constructional details of the gyrocompass are very complicated, a simpler "explanation" was devised. The 84 minutes arise from the formula 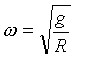 where g=32.2ft/s2 and R=the radius of the earth, 4000 miles. The formula for the natural frequency of a simple pendulum is 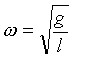 so that 84 minutes is the "period of a pendulum with a length
equal to the radius of the earth". A short pendulum with
l equal to a few feet, of which the upper
point of support is accelearated horizontally will swing back and
forth and hence its string will not be vertical. This, when
applied to a compass will give a wrong indication of verticality
to the device from which the operational error follows. Now if the
pendulum is 4000 miles long, consisting of a heavy point mass at
the center of the earth and the upper end of the (massless) string
at the surface (the earth not interfering with the string) it is
"clear" that we can move the top of the string horizontally in any
way we like, and the string being massless will always remain
radial, i.e., exactly vertical. This "simple explanation" is
misleading or no explanation at all for all sorts of
reasons. Aside from the fact that the earth would interfere with
the string or that the whole thing is physically unrealizable, the
value of g at the center
of the earth is zero, so that the string would be without
tension. The formula However, it is physically possible (although not practically feasible) to construct a mechanical pendulum of small size (3 feet or so) which has a period of 84 minutes. Such a pendulum has indeed the property that when its point of support is accelerated horizontally, it will not swing, but always remain exactly vertical. This property is true completely irrespective of the constructional details of the pendulum, whether it contains a gyroscope or not. The ship's gyrocompass is a very complicated pendulum indeed, but it still obeys this general property. It is no exaggeration to state that the "Schuler tuning" is essential to the proper operation of the compass, and indeed made the ship's compass practically possible. This was the 1920s. Since that day the 84 minute formula has
cropped up repeatedly in a variety of problems, some academic
without practical significance and others with spectacular
application. These appearances of the 84 minute value (
| |||||||||
| The Physical Pendulum | |||||||||
Let a pendulum be suspended at O and
let that point O be given
a horizontal acceleration 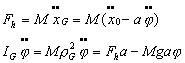 Eliminate the force Fh by substituting the first into the second equation : 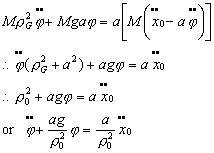 From the left hand side we see that the natural frequency of the physical pendulum is 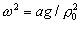 (1) The φ motion is forced by the right hand member. If the pendulum starts from rest (φ=0) it is seen that the angle φ is subjected to an initial acceleration 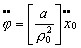 (2) proportional to the acceleration Now comes the trick. The point of suspension O,
experiencing 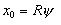 (3) where R is the radius of the earth. Satisfy yourself that the angle ψ is in the same direction as the "hang back" angle φ, and if by chance φ=ψ then the pendulum in its new location x0 is hanging exactly "vertical". Now differentiate (3) twice and substitute it into (2) : 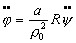 In order for the pendulum to remain "vertical" in its new location
φ
must equal ψ,
and since both start from zero,
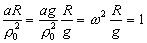 (4) Hence when the pendulum is tuned to ω2=g/R (which means that the dimensions be so chosen that g/R=ag/ρ02, the hang back angle φ due to the acceleration will be equal to the angle ψ necessary to keep the pendulum "vertical" in its new location. Problems
| |||||||||
| A Gyroscopic Pendulum | |||||||||
Consider a pendulum supported at O by a frictionless ball joint, allowing angular motions in any direction, carrying a gyrowheel with its spin axis along the pendulum stem. Let the gyrowheel mass be M, its moment of inertia about the spin axis be I=Mρ2, and let its angular momentum H=IΩ=Mρ2Ω, where Ω is the constant angular speed, and the vector is directed downward. For simplicity assume that the mass of the pendulum stem and non-rotating gyroframe is negligible with respect to the rotating gyro mass M. The point of support O of the gyropendulum is accelerated to the right by
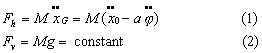 When the pendulum finds itself in the general position φ, θ , the moments of the external forces about the center of gravity are : 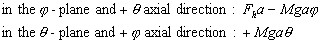 The rate of change of angular momentum to which these moments must be equated are: 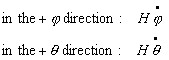 Hence, substituting equation (1), the equation of motion are 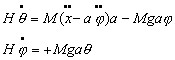 Before proceeding with these we remark that a gyroscope is very
tenaceous in holding its angular position.
Hence 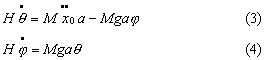 Eliminate θby substituting (4) into (3) : 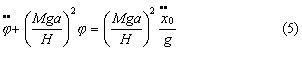 In the absence of acceleration  Now, when starting from rest (φ=0) the initial 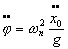 This is the "hang back" angle. In order for the pendulum to remain vertical afterwards we found in the previous section that this angular acceleration has to be 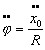 so that Schuler tuning requires that ωn2=g/R as before, or : 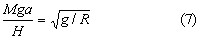 Now we like to know what this tuning formula means physically; in other words what is the required pendulum length a in terms of the other dimensions : 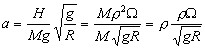 In this ρΩ is the peripheral speed of the gyrowheel at the radius of gyration which we make as high as possible, short of exploding the wheel by centrifugal force. A good figure for this speed is about 800 ft/sec. Hence 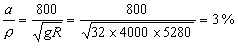 The pendulum length thus must be made very short: 3% of ρ or about 1% of the gyrowheel diameter. However this length is still a practical possibility, unlike the length found in Problem 2a. for the physical pendulum. Now we are ready to verify if our previous assumption that
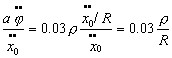 Here ρ is a few inches and R is 4000 miles, so that the simplification is amply justified. Problem 4This is Problem 2a. for the gyropendulum. Find what friction coefficient in the Ball joint (with radius ρ/1000) will freeze the aparatus, i.e., prevent the first θ motion at the onset of an acceleration. The actual gyroscopic ship's compass is a very complicated device. If its natural period is tuned to 84 minutes it becomes insensitive to accelerations of the base on which it is mounted. A complete explanation of this property takes some time and would disrupt the continuity of this essay. However it is the original structure for which the 84 minute period was devised and hence it is of importance. Therefore the explanation is given as an Appendix only. | |||||||||
| The Diametrical Hole Through the Earth | |||||||||
Before we can work this problem we must know the value of gat various depths in the earth. It is obvious that gcannot be constant throughout, because for reasons of symmetry gmust be zero at the center of the earth. Newton's gravitational law F=const·m1m2 is stated in terms of two particles (i.e., point objects without size) attracting each other. For larger objects the force can be calculated by integration over all particles. The results of such an integration for the case of uniform density distribution(which is not simple : Problem 5 and 6) are shown in the figure, where the value of g is plotted as a function of distance from the center (of course the direction of gis always radial). Inside the earth the relation is linear or g=g0r/R where g0=32.2ft/s2 and R=4000 miles. The actual density distribution in the earth is far from uniform; the center core is more than twice as dense as the outer mantle, which makes the actual g distribution a non-linear function of r . Here we will discuss a uniform earth only. Outside the earth the relation is as if the earth were replaced by a single concentrated point mass at its center: 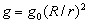 This is true for any symmetrical density distribution f(r). Problem 5Prove that the Newtonian gravitational attractive force between a mass particle and a thin walled hollow sphere is zero when the particle is located inside the sphere, while for a particle outside the sphere the force is equal to that for the case that the entire sphere mass is concentrated in its center. (See figure for hint.) Find the force between P and an element at Q in terms of the letters r and φ. Integrate over the thin ring dφ for constant φ and constant r. This semi-integrated force by symmetry is directed along OP. Then write the integral over the sphere for φ from 0 to 180°. The evaluation of this integral is very messy, but it is much simplified if you first express r as a function of φ then differentiate this relation and substitute the result into the integral, which then becomes an integral of f(r)dr, not containing the letter φ Problem 6With the theorem of Problem 5 derive the fact that for a solid sphere of constant density the gravitational acceleration g is a linear function of the radius, rising from zero at the center to g0 at the surface. Now the problem of the falling stone. If the hole is along the polar axis of the earth, rotation of the earth is irrelevant. At depth r from the center the force is mg=mg0r/R towards the center. Hence: 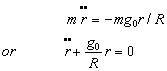 This is the simple vibration equation and the stone will execute harmonic vibrations with a frequency ωn2=g0/R about the center. The frequency is independent of the amplitude and rmax=R is the special case where the stone takes 42 minutes to go from one surface pole to the other. If the hole is not passing through the poles, Coriolis effects from the earth rotation come in and the free unrestrained path of motion will not be a straight line. If a straight, frictionless guide is provided the above answer is true for a diametral hole at any angle with the polar axis. | |||||||||
| Particle on a Straight Surface Track | |||||||||
The gravity force on a particle m at P, directed along PC is : mg=mg0R2/r2 The component of this force along OPis x/r times as small 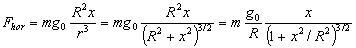 Hence the equation of track motion is for no friction 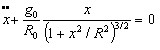 a nonlinear equation giving a natural frequency of vibration depending on the amplitude xmax. For small vibrations x<<R, this linearizes to: 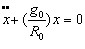 so that for small amplitudes (i.e., x less than 10 miles) the natural frequency is ω2=g0/R and the period is 84 minutes. Problem 7
Problem 8Taking the complete non-linear equation of motion, by making the substitution: 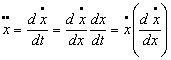 (which is usual with non-linear second order differential equations) derive the first integral : 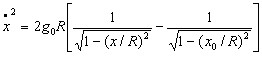 where x0 is the maximum amplitude
of vibration. The "phase plane diagram" plots of
Problem 9By the standard method of non-linear vibration carry out the second integration of the previous problem with the following result for the period of vibration T: 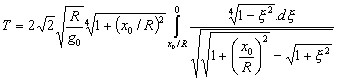 | |||||||||
| Motion in Tunnel at Arbitrary Angle | |||||||||
Let a tunnel be cut through the earth so that its center point O is at distance a from the earth's center C. Consider a particle m at P sliding without friction along the tunnel. Let OP=x and CP=r. The gravity force on m, directed along PC is mg=mg0r/R The component of this force along the track is
x/r times as small or
mg0r/R. This force equals
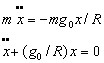 and the natural frequency of oscillation is
| |||||||||
| Earth Satellites | |||||||||
Let a satellite move in a circular orbit at height habove the earth's surface. It is in d'Alembert's equilibrium when the centrifugal acceleration ω2r=ω2(R+h) equals the gravitational acceleration 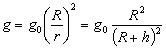 Equating these two quantities gives 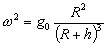 which determines the period of the satellite. For a roof top satellite h<<R and the above expression reduces to ω2=g0/R with an 84 minute period. The above expression can be written as : 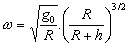 The period of the satellite becomes larger than 84 minutes
at increased heights h, and is found from 84 minutes by multiplying that quantity by
( For example if we desire a 24 hour satellite for communication purposes we have
and h=5.6R=22,400miles Problem 10What is the distance between the center of the earth and the center of the moon, expressed in earth radii ? | |||||||||
| Moon and Planet Satellites | |||||||||
All problems discussed so far have been with respect to the earth, assumed to be of uniform density. The answer to all has been so that we can conclude that the 84 minute period remains at that value for all other moons, planets or suns for which the ratio g0/R is the same as on earth. Now let us look at a point in the interior of the earth and divide the earth into a solid sphere up to our point and a hollow sphere around it. Our point is a surface point for both, being on the inner surface of the hollow sphere. The g-value at our point is the integral of all attractions to all points. Now by the theorem of Problem 5 the g at our point caused by the outer hollow sphere is zero, and whatever g there is, is caused entirely by the solid inner core. Since in the interior of the (uniform density) earth g=g0r/R, this means that we can shave off the earth a crust of any thickness we like, and on the surface of the remaining core g/r=g0/R0. Hence we conclude that the 84 minute period in all previous problems is preserved for all planets or moons which have the same density as the earth. For a planet or moon of less density, the value of R is the same, but g0 is diminished proportional to the density. Therefore the value of ω2 is directly proportional to the density of the planet only, and the period Tis inversely proportional to the square root of the density. The moon's density is 0.607 times the density of the earth. Hence the characteristic period for the moon (for all applications discussed here) is (84 minutes)(1/0.607)1/2=108 minutes Problem 11Assume that the earth is made of two materials, an inner spherical core and outer hollow spherical mantle. Assume that the core density is twice the mantle density. The values of R and g0 are obviously the ones we observe. The outer radius of the core is 0.618R.
| |||||||||
| Inertial Navigation | |||||||||
An inertial navigation or inertial guidance device is a combination of three essential elements : first a platform which keeps its direction fixed in inertial space (by means of gyroscopes now or possibly by other means in the future); second a number of accurate accelerometers, in various directions; third a computer which integrates the output of the accelerometers and thus keeps track of velocity, location and angular position in space of the accelerometers. The details of the arrangement of these elements into the whole differ with the application. For ship navigation on or near the surface of the earth (the ocean) there are two accelerometers only, one always directed NS, the other always EW. When the ship moves from place to place, or even when it is standing still at the dock these NS and EW directions continually change with respect to absolute space, caused both by the ship's motion and by the rotation of the earth. One of the duties of the computer is to keep track of all this and to give commands to servometers which continually change the position of the accelerometer platform relative to the steady inertial platform. A third accelerometer (in the vertical direction) serves no purpose, since it would measure g only. Hence only two are used, while for space navigation three are necessary. The accuracy whereby the accelerations have to be measured is phenomenal, a very slight error in the measured acceleration becomes a very large error in position when integrated twice over long time intervals. Problem 12If one (horizontal) accelrometer has a fixed error, reading the acceleration high by one millionth of g, calculate the error in the ship's position after 3 days. One very serious source of possible error is a slight tilt of the accelerometer platform from the horizontal. In that case the accelerometer not only feels the acceleration of the ship, but also a component of gwhich it cannot distinguish from a ship's acceleration. When adjusting the apparatus at dockside prior to a voyage the accelerometers have to be set horizontal to give zero reading. However this can be done to a certain accuracy only and the ship may go out with an initial tilt of the accelerometer of one part in a million or so. On a flat earth this error would remain right in the system with the disastrous results of above Problem 12. However on a curved earth the tilt at dockside does not remain constant. This is because the accelerometer measures an acceleration (due to tilt) which it interpretes as ship's acceleration and hence as ship's displacement after two integrations. When the computer believes that the ship is a few miles from the dock to which it is actually moored it concludes that the platform has to be turned through a small angle to be perpendicular to the new vertical in the new in the new (spurious) location. The result is that with a live computer circuit the table oscillates about the true horizontal position (with the inevitable 84 minute period). The computer conculdes that the ship sails back and forth with an 84 minute period, instead of concluding that it sails in one direction with a constant (small) steady acceleretion, piling up a fantastic velocity and displacement in the course of days. The analysis is as follows : with the ship at dockside, while the true actual acceleration is zero, let the tilt angle be φ (a function of time) with the consequent indicated acceleration gφ. The computer integrates this into a displacement we will call x (also a function of time). The computer then gives a command to tilt the platform back through angle x/R (being the angle between the true verticals at the dock and at the presumed position x). If the original tilt at time zero is φ0 then the actual tilt angle of the platform is φ=φ0-x/R, and the indicated acceleration is 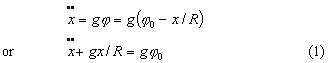 Thus the indicated position is seen to oscillate with period ω2=g/R. To find the differential equation of the tilt angle φ we differentiate (1) twice 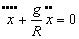 With  The intial conditions are that at
t=0 the platform angle
φ=φ0 and the indicated distance from dockside
x=0, and of course In case the earth were flat no Schuler tuning effect would exist and the x(t) diagram would be the osculating parabola to the sine curve, shown dotted in the graph. It is seen that the automatic Schuler tuning saves the day and that without it inertial navigation on earth over prolonged periods of time would be next to nigh impossible. Problem 13Calculate the maximum indicated displacement for an intial error angle of :
| |||||||||