![]() Definition and Formulae :
Definition and Formulae :
The variance is a measure of how spread out a distribution is. It is computed as the average squared deviation of each number from its mean. For example, for the numbers 1, 2, and 3, the mean is 2 and the variance is:
The formula (in summation notation for the variance in a population is
where m is the mean and N is the number of scores.When the variance is computed in a sample, the statistic
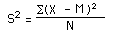
(where M is the mean of the sample) can be used. S2 is a biased estimate of s2, however. By far the most common formula for computing variance in a sample is:
which gives an unbiased estimate of s2. Since samples are usually used to estimate parameters, s2 is the most commonly used measure of variance.
The formula for the standard deviation is very simple: it is the square root of the variance. It is the most commonly used measure of spread.
If variable Y is a linear transformation of X such that: Y = bX + A, then the variance of Y is: b2σx2 whereσx2 is the variance of X. The standard deviation of Y is b sx where sx is the standard deviation of X.
![]() Illustrations :
Illustrations :
The following example shows how to calculate the variance for different heights of people. The first step is to find out the mean (M) of the population. N is the number of samples in the population and X is the height of each sample.
![]() Applications :
Applications :
An important attribute of the standard deviation as a measure of spread is that if the mean and standard deviation of a normal distribution are known, it is possible to compute the percentile rank associated with any given score. In a normal distribution, about 68% of the scores are within one standard deviation of the mean and about 95% of the scores are within two standards deviations of the mean.
The standard deviation has proven to be an extremely useful measure of spread in part because it is mathematically tractable. Many formulas in inferential statistics use the standard deviation.
Although less sensitive to extreme scores than the range, the standard deviation is more sensitive than the semi-interquartile range. Thus, the standard deviation should be supplemented by the semi-interquartile range when the possibility of extreme scores is present.
Standard Deviation as a Measure of Risk
The standard deviation is often used by investors to measure the risk of a stock or a stock portfolio. The basic idea is that the standard deviation is a measure of volatility: the more a stock's returns vary from the stock's average return, the more volatile the stock. Consider the following two stock portfolios and their respective returns (in per cent) over the last six months. Both portfolios end up increasing in value from $1,000 to $1,058. However, they clearly differ in volatility. Portfolio A's monthly returns range from -1.5% to 3% whereas Portfolio B's range from -9% to 12%. The standard deviation of the returns is a better measure of volatility than the range because it takes all the values into account. The standard deviation of the six returns for Portfolio A is 1.52; for Portfolio B it is 7.24.
![]() Applet :
Applet :
For an illustration of variance go to
http://www.math.uah.edu/psol/applets/VarianceTestExperiment.htm
![]() Excel Function :
Excel Function :
These functions can be accessed by clicking on Insert and then choosing Function from the drop down menu.
The Excel function for finding a Studen'ts T distribution for a given data set is :
VAR(number1,number2,...)
Estimates variance based on a sample (Ignores logical values and text in the sample)