
Conservation of Mass
In the Reynolds transport theorem for conservation of mass, let B = m, i.e. Bsys = msys = mass of the system,

For our system, we know that

So, Reynold's Transport Theorem (R.T.T.) becomes

OR,




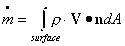 = mass
flow rate outward through a surface
= mass
flow rate outward through a surface 




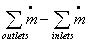





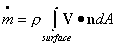
 where mass flow
rate = density X volume flow rate
where mass flow
rate = density X volume flow rate
Consider an outlet:
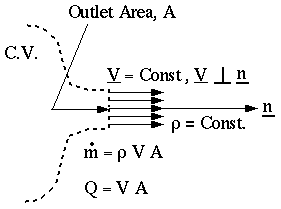
 and
and 
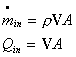
….since the negative sign is accounted for in
the conservation of mass equation,
i.e. 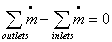
If an inlet or exit is not 1-D, we can still
use  but VAV must be the average
velocity
but VAV must be the average
velocity


but for most problems V is parallel to n……

An equivalent 1-D outlet will have the same mass flow
rate as the actual outlet.
A container of water,
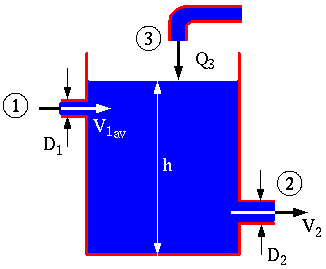
Given: VAV,
Q3, D1, D2 and h equal constants.
V1 = 3 m/s; Q3 = 0.01 m3/s; h = constant;
D1 = 0.05m; D2= 0.07m
Find: Average exit velocity
V2
Solution: Use conservation
of mass. First draw the C.V. shown.
Since it is steady and incompressible, 


