- In total, there are seven primary dimensions. Primary (sometimes called basic) dimensions are defined as independent or fundamental dimensions, from which other dimensions can be obtained.
- The primary dimensions are: mass, length, time, temperature, electric current, amount of light, and amount of matter. For most mechanical and thermal science analyses, however, only the first four of these are required. The others will not be of concern to most mechanical engineering analyses.
- In order to assign numbers to these primary dimensions, primary units must be assigned.
These are listed in the table below for the three unit systems:
Primary Dimension
Symbol
SI unit
BG unit
English unit
mass
m (sometimes M)
kg (kilogram)
slug
lbm (pound-mass)
length
L (sometimes l)
m (meter)
ft (foot)
ft (foot)
time
t (sometimes T)
s (second)
s (second)
s (second)
temperature
T (sometimes q )
K (Kelvin)
o
R (degree Rankine)R (Rankine)
electric current
I (sometimes i)
A (ampere)
A (ampere)
A (ampere)
amount of light
(luminous intensity)C (sometimes I)
c (candela)
c (candela)
c (candela)
amount of matter
n or N (sometimes
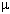 )
) mol (mole)
mol (mole)
mol (mole)
- All other dimensions can be derived as combinations of these seven primary dimensions.
These are called secondary dimensions, with their corresponding secondary units.
A few examples are given in the table below:
Secondary Dimension
Symbol
SI unit
BG unit
English unit
force
F (sometimes f)
N (Newton = kg× m/s2)
lbf (pound-force)
lbf (pound-force)
acceleration
a
m/s2
ft/s2
ft/s2
pressure
p or P
N/m2, i.e. Pa (Pascal)
lbf/ft2 (psf)
lbf/in2 (psi) (note: 1 ft = 12 in)
energy
E (sometimes e)
J (Joule = N× m)
ft× lbf (foot pound)
ft× lbf (foot pound)
power
P
W (watt = J/s)
ft× lbf/s
ft× lbf/s
- Note that there are many other units, both metric and English, in use today. For example, power is often expressed in units of Btu/hr, Btu/s, cal/s, ergs/s, or horsepower, in addition to the standard units of watt and ft× lbf/s. There are conversion factors listed in many textbooks to enable conversion from any of these units to any other.
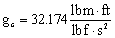
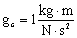
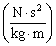
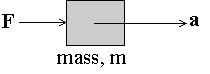
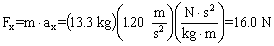
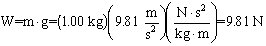 .
.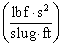 or
or 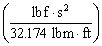 or
or 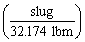
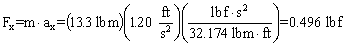
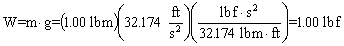 .
.