The Energy Equation for Control Volumes
- Recall, the First Law of Thermodynamics:
 where
where  = rate of change of total energy of the system,
= rate of change of total energy of the system,  = rate of heat added to the system,
= rate of heat added to the system,  = rate of work done by the system
= rate of work done by the system
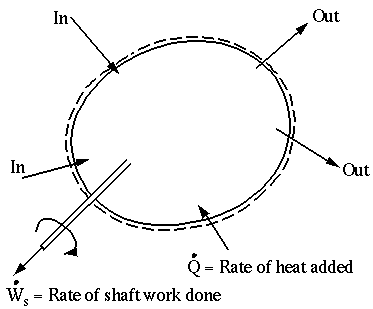
- In the Reynolds Transport Theorem (R.T.T.), let
 .
.
So, 
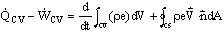
The left side of the above equation applies to the system, and the right side corresponds to the control volume. Thus, the right side of the above equation can be called the General Integral Equation for Conservation of Energy in a Control Volume,
where e = total energy of the fluid per unit mass,  ,
,  = internal energy per unit mass,
= internal energy per unit mass, 
= kinetic energy per unit mass, gz = potential energy per unit mass.
- Generally, what is done is to split the work term up into 3 parts:
 , where:
, where:  = rate of shaft work,
= rate of shaft work,  = rate of pressure work,
= rate of pressure work,  = rate of viscous work.
= rate of viscous work.
Note: 
has dimensions of {work/time} = Power (so these are actually power terms). Let's look at each of these terms individually:
- Rate of Shaft Work,

= rate of work done by the fluid on a shaft protruding outside the C.V.
E.g. a turbine (extracts energy from a flow) : The turbine takes energy from the fluid and converts it into rotation of the shaft.
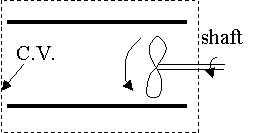
Note:  is positive for a turbine (work done by the fluid), and
is positive for a turbine (work done by the fluid), and  is negative for a fan (work done on the fluid).
is negative for a fan (work done on the fluid).
- Rate of Pressure Work
,  = rate of work done by pressure forces at the control surface
= rate of work done by pressure forces at the control surface
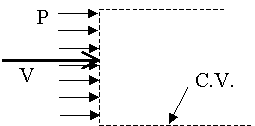
It turns out that  .
.
- Rate of viscous work
,  = rate of work done by viscous stresses at the control surface. If we define vector
= rate of work done by viscous stresses at the control surface. If we define vector as the resultant shear stress acting on the C.S., it turns out that
as the resultant shear stress acting on the C.S., it turns out that  . Note: For now,
. Note: For now,  is usually zero
is usually zero
- Plug all of these back into the energy equation, but put the pressure work term on the right hand side:
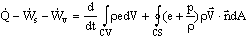
But  , and from the definition of enthalpy (per unit mass),
, and from the definition of enthalpy (per unit mass),  . Plugging these into the above equation yields
. Plugging these into the above equation yields

.
This is The general equation of conservation of energy for a fixed control volume.
- Viscous work term
:
For a lot of problems,  . As an example of a case where this is not the case, i.e. a case in which
. As an example of a case where this is not the case, i.e. a case in which  , consider the control volume sketched below in which part of the control surface lies along a moving wall with friction. (The top wall is moving, but the bottom wall is fixed.)
, consider the control volume sketched below in which part of the control surface lies along a moving wall with friction. (The top wall is moving, but the bottom wall is fixed.)
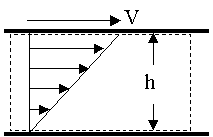
On the top surface of the control volume, , so,
, so,  .
.
I.e., viscous work is being done by the moving wall on the fluid.
- Cases where
 = 0: Recall when we talked about the momentum equation, we had a
= 0: Recall when we talked about the momentum equation, we had a  term that was hard to evaluate. Fortunately, we could either eliminate it by proper choice of C.V. or let it be the unknown. A similar thing happens in the energy equation.
We have,
term that was hard to evaluate. Fortunately, we could either eliminate it by proper choice of C.V. or let it be the unknown. A similar thing happens in the energy equation.
We have, 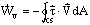
, which is a complicated and ugly term to try to evaluate. But for most control volumes that we will deal with, it turns out to be zero. Here are some examples:
- Along a stationary solid wall
:
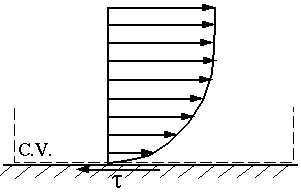
Along this wall, since there is friction acting,  (i.e. there is a shear stress acting on the fluid.) But,
(i.e. there is a shear stress acting on the fluid.) But,  (no slip condition at a wall!), i.e.
(no slip condition at a wall!), i.e.  .
.
Analogy - Think back to high school physics class when you first learned about the concept of work. My teacher pushed on the wall with all his might and said, "How much work am I doing?" Answer: None! Work = Force x Distance. Here there is a force, but no distance. For flow along a stationary solid wall, it is the same - there is a force (per unit area) which is  , but no motion
, but no motion  . Thus, the net viscous work along this wall is zero.
. Thus, the net viscous work along this wall is zero.
- When moving walls are totally enclosed by the C.V.
For example, consider the blades of pumps or turbines
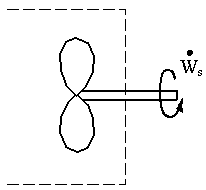
In this case, if the control surface is taken along the walls of the blades,  . However, we can draw the C.V. around the whole thing! We simply include all of the viscous and pressure work terms on these blades as part of
. However, we can draw the C.V. around the whole thing! We simply include all of the viscous and pressure work terms on these blades as part of  .So here, even though
.So here, even though  is not zero along the blades themselves, we can avoid evaluating the integral since we include it in
is not zero along the blades themselves, we can avoid evaluating the integral since we include it in  , which is usually either a given or an unknown in the problem. So
, which is usually either a given or an unknown in the problem. So on our chosen C.V. (surrounding the turbine), but
on our chosen C.V. (surrounding the turbine), but  . In other words, we can lump all the viscous work terms together into one term, and call it
. In other words, we can lump all the viscous work terms together into one term, and call it  .
.
- At one -dimensional inlets or outlets
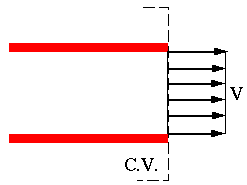
Here,  . Therefore the viscous work term must be zero
. Therefore the viscous work term must be zero  .
.
- Normal to streamlines in a sheared parallel flow
Even if we have a non-one-dimensional inlet or outlet, i.e. slice right across an outlet
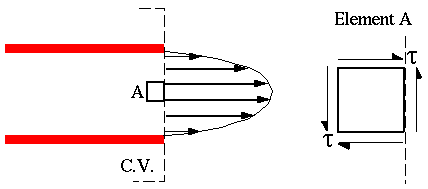
 (by definition of the dot product). So, in this case too,
(by definition of the dot product). So, in this case too,  .
.
- In the unsheared part of the flow
(far away from the walls, for example)
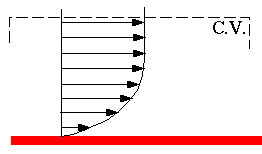
Viscous stresses are very large in the boundary layer near the wall, however far away from the wall,  .
.
- BOTTOM LINE: By "wise" choice of C.V., we can usually avoid having to calculate
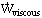
term.
Simplifications of the Energy Equation
- If steady flow, with one-dimensional inlets/outlets
The energy equation reduces to

NOTE: This is identical to the energy equation used in ME30: You called it the First Law for a C.V. for Steady-State, Steady-Flow (SSSF). In thermodynamics class, you should remember lots of examples - i.e. turbines, pumps, compressors, throttle valves, condensers, etc.
Example Problem:
Given: An air compressor
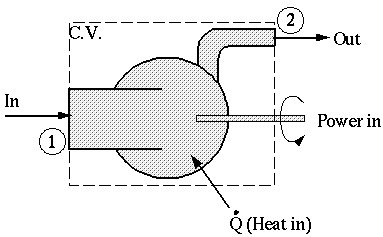

Find:  , how much heat is transferred into the compressor (in BTU/hr)? Note: We expect
, how much heat is transferred into the compressor (in BTU/hr)? Note: We expect  to be negative, since heat is given off by the compressor)]
to be negative, since heat is given off by the compressor)]
Solution: Draw a C.V. around the entire thing (not shown on the sketch), with the shaft protruding out from the C.S.
- Energy Equation
: Assume steady with 1-D inlets and outlets (only one inlet and one outlet here)
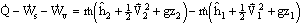
By wise choice of control volume,  . Also, gz1 and gz2 can be neglected because potential energy for air is generally negligible, especially in a case like this where there is a lot of heat transfer and corresponding change in enthalpy. The inlet velocity,
. Also, gz1 and gz2 can be neglected because potential energy for air is generally negligible, especially in a case like this where there is a lot of heat transfer and corresponding change in enthalpy. The inlet velocity,  can also be neglected here. With these simplifications, the energy equation becomes
can also be neglected here. With these simplifications, the energy equation becomes

- But air is an ideal gas, and from thermodynamics,
 . Thus,
. Thus,  , and the heat transfer becomes
, and the heat transfer becomes  . This is the answer in variable form; all that remains is to plug in the numbers.
. This is the answer in variable form; all that remains is to plug in the numbers.
- Numbers
: This is a lesson in English units!
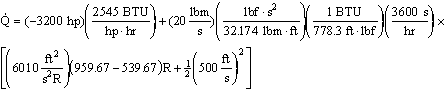
which gives a final answer of  .
.
- Comments
:  is negative because heat is given off by a compressor. This is a huge compressor. A typical window air conditioner can cool 5000 BTU/hr. The above answer is 100 times that!
is negative because heat is given off by a compressor. This is a huge compressor. A typical window air conditioner can cool 5000 BTU/hr. The above answer is 100 times that!
Kinetic Energy Flux Correction Factor
As was done with the momentum equation, a correction factor for the velocity term (kinetic energy term) in the energy equation must be introduced to account for non-uniform inlets and exits. Consider again an actual versus equivalent one-dimensional outlet, as sketched:
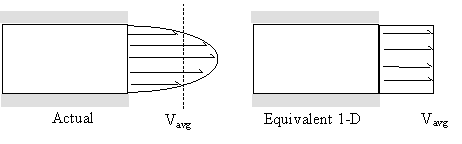
- Recall that,
 . In the energy equation, consider the kinetic energy flux term,
. In the energy equation, consider the kinetic energy flux term,  . Because of the V3 term here, the integrand is non-linear and thus it turns out that
. Because of the V3 term here, the integrand is non-linear and thus it turns out that
(Kinetic energy flux)actual > (Kinetic energy flux)equiv.
- So, define a kinetic energy flux correction factor as:
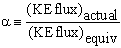
Mathematically,  .
.
- Just as we did in the momentum equation, we can put this correction factor into the energy equation, and then treat all inlets and outlets as though they were one-dimensional, with average velocity Vav. With this correction, the general steady-state, steady flow (SSSF) form of the energy equation for a fixed control volume becomes:

- Some values of
 , and some comments:
, and some comments:
- Uniform (1-D) inlet/exit
 = 1.0
= 1.0
- Fully developed laminar pipe flow
 = 2.0
= 2.0
- Fully developed turbulent pipe flow
 = 1.04 - 1.11 (depends on Reynolds Number - if Reynolds number is unknown, I usually let
= 1.04 - 1.11 (depends on Reynolds Number - if Reynolds number is unknown, I usually let  = 1.06)
= 1.06)
- So for turbulent flow,
 does not affect the solution too much. But, for laminar flow,
does not affect the solution too much. But, for laminar flow,  is very important.
is very important.
- Note
: Even for turbulent flow, where the kinetic energy flux correction factor is not real important, it is always best to keep  in the equation.
in the equation.
"Head" Form of the Energy Equation
- This will be the most useful form for pipe flow problems and civil engineering problems (hydroelectric dams, pumping systems, etc.)
- Assume:
- One inlet (may or may not be one-dimensional)
- One outlet (may or may not be one-dimensional)
- Steady-state, steady-flow (SSSF)
- Some pumps and turbines enclosed by the control volume (with shafts protruding out of the control surface)
- Some heat transfer
- "Wise" control volume chosen such that the viscous power term,
 . (Recall, as long as our control surface does not lie along a moving wall with friction, this viscous work term will be identically zero.)
. (Recall, as long as our control surface does not lie along a moving wall with friction, this viscous work term will be identically zero.)
- Consider a general control volume as sketched below:
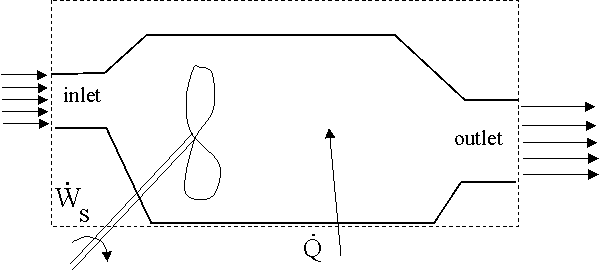
Assume the following variables at the inlet and outlet: A (cross-sectional area), Vav (average velocity across the area), p (pressure), T (temperature),  (specific enthalpy) and
(specific enthalpy) and  (density). In addition, the elevations (z) at the inlet and outlet are known.
(density). In addition, the elevations (z) at the inlet and outlet are known.
- The energy equation is
 ,
,
but the viscous work term will be zero.
- To get the above equation in the form of a head, divide each term by
 , which will make the dimension of each term equal to length (or head, which is desired). Also, use the definition of specific enthalpy,
, which will make the dimension of each term equal to length (or head, which is desired). Also, use the definition of specific enthalpy,  . The equation becomes
. The equation becomes
 , or rearranging,
, or rearranging,
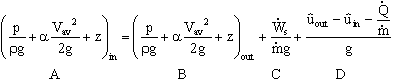
- The group of terms on the left (A) represents the total head at the inlet. The first group of terms on the right (B) represents the total head at the outlet. The next term (C) is the shaft work term expressed as a head, and the last group of terms (D) represents heat transfer and change of internal energy expressed as a head.
- Let us consider the last term more carefully. If there are no irreversible losses in the flow, any heat added will increase the internal energy of the fluid. Likewise, any heat lost will decrease the internal energy of the fluid. It turns out, then, that term D in the above expression is identically zero if there are no irreversible losses. In real life, of course, there are always irreversible losses. For example, friction, mixing, and heat transfer through a finite temperature difference all contribute to an irreversible loss of useful energy. (This is related to the second law of thermodynamics.) Thus, it turns out that the head loss term is always positive for any real flow, i.e.
 .
.
- Now consider term C in the head form of the energy equation above. Recall that
 is positive for turbines and negative for pumps. Since term C has dimensions of length, i.e. head, we can define the following positive heads for pumps and turbines:
is positive for turbines and negative for pumps. Since term C has dimensions of length, i.e. head, we can define the following positive heads for pumps and turbines:
 and
and 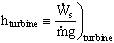
Because of the negative sign in the first of these equations, both hpump and hturbine are always positive quantities by convention.
- Finally, plugging in our expressions for hlosses, hpump, and hturbine, the head form of the energy equation becomes
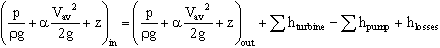 ,
,
where the summation signs are included since there can be more than one pump and more than one turbine within the control volume. This form of the energy equation is the most useful form for a great variety of problems. Keep in mind, of course, the limitations imposed by the set of assumptions listed above.
Efficiencies of Pumps and Turbines
- Consider for example a pump, as sketched, with a control volume (dashed line) around the entire pump:
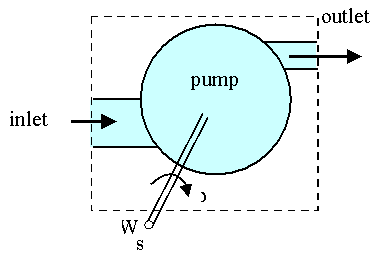
In the sketch,  is the angular velocity of the rotating shaft which drives the pump. The shaft power,
is the angular velocity of the rotating shaft which drives the pump. The shaft power,  , is negative since work is being done on the control volume. Also, let T be defined as the torque on the rotating shaft. Here are some necessary definitions:
, is negative since work is being done on the control volume. Also, let T be defined as the torque on the rotating shaft. Here are some necessary definitions:
- Define BHP = brake horsepower, i.e. the actual shaft power supplied to the pump through the rotating shaft. From physics we recall that the power of a rotating shaft is
 . By convention, BHP is by convention always a positive value. Note that the term "horsepower" has made its way into the literature, and is retained even if working in SI units.
. By convention, BHP is by convention always a positive value. Note that the term "horsepower" has made its way into the literature, and is retained even if working in SI units.
- Also define WHP = water horsepower, i.e. the useful power supplied to the fluid due to the pump. By convention, WHP is also by convention always a positive value.
- Because of losses (friction, turbulent mixing, irreversible heat transfer), the water horsepower is always less than the brake horsepower (WHP < BHP for a pump). In other words, the actual useful power supplied to the fluid by the pump is always less than the power required to drive the pump's shaft. The pump's efficiency can therefore be defined as follows:
 .
.
Because of losses,  .
.
- For a turbine, the useful output of the turbine is the brake horsepower; the required power from the fluid, the water horsepower, is always greater than the brake horsepower due to inefficiencies of the turbine. Note again that both WHP and BHP are defined by convention as positive. Turbine efficiency is defined as:
 .
.
Because of losses,  .
.
- How then do these power terms and efficiencies get introduced into the head form of the control volume conservation of energy equation? It turns out that there are two possible ways to treat pump and turbine losses.
- The thermodynamicist's way is to let
 in the energy equation be the actual brake horsepower (-BHP for a pump and BHP for a turbine) of the rotating shaft, and then include any pump losses (inefficiencies) in the hlosses term of the equation.
in the energy equation be the actual brake horsepower (-BHP for a pump and BHP for a turbine) of the rotating shaft, and then include any pump losses (inefficiencies) in the hlosses term of the equation.
- The fluid dynamicist's way is to let
 be the water horsepower (-WHP for a pump and WHP for a turbine), and then to ignore pump losses in the hlosses term. Instead, the efficiencies defined above are used to calculate actual brake horsepower when needed. This way is the convention we will follow.
be the water horsepower (-WHP for a pump and WHP for a turbine), and then to ignore pump losses in the hlosses term. Instead, the efficiencies defined above are used to calculate actual brake horsepower when needed. This way is the convention we will follow.
- In summary, following the fluid dynamics convention, the final, most useful formulation of the energy equation in head form is
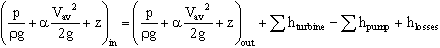
where  and
and  .
.
Brake horsepower is then calculated by  and
and  .
.
Example Problem
Given:
A pump is used to draw water from a large reservoir as sketched. The water shooting out the nozzle at the pump outlet has uniform velocity V2, volume flow rate Q, and inner exit diameter D2.
Insert Image pumpabove.gif
Also known in the problem are pipe diameter D, pump efficiency  , hlosses, and the elevations z0, z1, and z2. Note that hlosses represents irreversible head losses due to friction in the pipe and due to turbulent mixing and other irreversible losses in the pipe elbow and the inlet region of the pipe. At this point in our study, we do not know how to calculate these, but later on we will learn how to estimate these head losses.
, hlosses, and the elevations z0, z1, and z2. Note that hlosses represents irreversible head losses due to friction in the pipe and due to turbulent mixing and other irreversible losses in the pipe elbow and the inlet region of the pipe. At this point in our study, we do not know how to calculate these, but later on we will learn how to estimate these head losses.
Find:
(a) WHP (water horsepower) actually delivered to the water by the pump.
(b) BHP (brake horsepower) required to run the pump.
Solution:
- (a) The first step in any control volume solution is to pick a control volume. As always, we want to pick a wise control volume which leads to the least amount of algebra. Here, and in most control volume problems involving a large reservoir, cut the control surface just below the free surface of the reservoir, where the pressure is known (patm) and the inlet velocity is negligible (since the reservoir is so large). Call this the inlet, 1, of the control volume.
Insert Image pumpabcv.gif
As shown, the control volume surrounds the pump and the pipe, and cuts through the outlet at location 2.
- Use the conservation of mass equation for
 = constant.
= constant.
 where
where  , which leads to Q2 = Q1 = Q (Q is given in the problem statement).
, which leads to Q2 = Q1 = Q (Q is given in the problem statement).
- Solve for V2 (Note that here, V2 = V2av, since the exit velocity is uniform.):
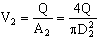
- Also:
 but since
but since  . This is a direct result of our wise choice of control volume, and will reduce the complexity of the energy equation significantly.
. This is a direct result of our wise choice of control volume, and will reduce the complexity of the energy equation significantly.
- Now we use the head form of the energy equation to find the water horsepower
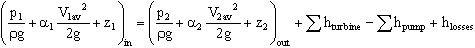
Here p1=p2=patm so the pressure terms cancel out. As mentioned above, V1av is negligible at the free surface of the large reservoir. Finally, there are no turbines here, and only one pump, with hpump defined as  . The head losses are known from the problem statement; solving for WHP, the energy equation thus reduces to
. The head losses are known from the problem statement; solving for WHP, the energy equation thus reduces to
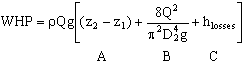
- Physically, the pump power may be thought of in this manner: the pump supplies power to the water for three purposes:
- to raise the elevation of the water (term A)
- to increase the speed (kinetic energy) of the water (term B)
- to overcome friction and other irreversible losses in the flow. (term C)
- (b) Actual shaft power required will be greater than WHP due to inefficiencies of the pump.
 .
.
- Note: The actual electrical power needed to run this pump will be even greater than the brake horsepower due to motor inefficiency.
Example Problem
Given: A small water pipe flow rig:
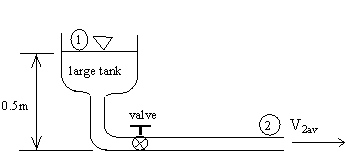
Suppose we know that hlosses = 0.4 m = total head loss due to valve losses, pipe friction, elbow losses, etc. (Later on we will learn how to estimate these.)
Find: V2av (average velocity at pipe exit)
Solution:
- First pick and draw the C.V.
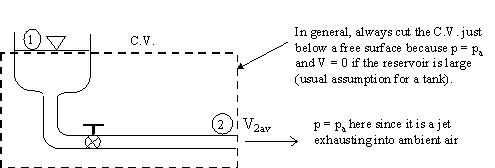
- Apply the head form of the energy equation. Note that this problem is not exactly steady, but if the tank is large, we can assume negligible unsteady effects for the first few moments of time at least. We refer to such conditions as "pseudo-steady" or "quasi-steady", and simply invoke the SSSF (steady-state, steady flow) simplification of the energy equation for a control volume:
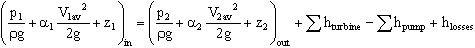
- Here, several terms in the above equation go away. The pressure terms cancel since p1 = p2 = patm. The average velocity at the inlet, 1, is very small since the tank is assumed to be large. There are neither pumps nor turbines in this control volume, so those two terms are zero.
- With the terms which remain, solve for V2av:
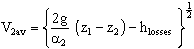
- The above equation is the answer in variable form. Let us now examine the importance of kinetic energy flux correction factor in this problem. At this point, nothing has been said as to the nature of the flow, i.e. if it is laminar or turbulent. If the flow remains laminar, and the pipe is long enough for fully developed flow at the outlet,
 , and V2av becomes
, and V2av becomes
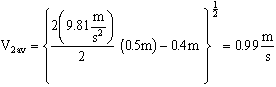
- If the flow in the pipe is instead turbulent,
 , and V2av becomes 1.36 m/s.
, and V2av becomes 1.36 m/s.
- If the kinetic energy flux correction factor at the outlet is ignored, i.e. if
 , the answer for both laminar and turbulent flow becomes V2av = 1.40 m/s.
, the answer for both laminar and turbulent flow becomes V2av = 1.40 m/s.
- Comparing these results with different values of the kinetic energy flux correction factor, it is obvious that for laminar pipe flow,
 should not be ignored, since it makes a big difference in the solution (here around 40%!). For turbulent flow, since
should not be ignored, since it makes a big difference in the solution (here around 40%!). For turbulent flow, since  is so close to unity, it is often ignored. However, it is wise to include it in all calculations for better accuracy.
is so close to unity, it is often ignored. However, it is wise to include it in all calculations for better accuracy.
 where
where  = rate of change of total energy of the system,
= rate of change of total energy of the system,  = rate of heat added to the system,
= rate of heat added to the system,  = rate of work done by the system
= rate of work done by the system  .
.
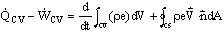
 ,
,  = internal energy per unit mass,
= internal energy per unit mass, 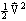
 , where:
, where:  = rate of shaft work,
= rate of shaft work,  = rate of pressure work,
= rate of pressure work,  = rate of viscous work.
= rate of viscous work.


 is positive for a turbine (work done by the fluid), and
is positive for a turbine (work done by the fluid), and  is negative for a fan (work done on the fluid).
is negative for a fan (work done on the fluid).
 = rate of work done by pressure forces at the control surface
= rate of work done by pressure forces at the control surface
 .
.
 = rate of work done by viscous stresses at the control surface. If we define vector
= rate of work done by viscous stresses at the control surface. If we define vector as the resultant shear stress acting on the C.S., it turns out that
as the resultant shear stress acting on the C.S., it turns out that  . Note: For now,
. Note: For now,  is usually zero
is usually zero
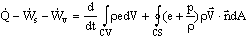
 , and from the definition of enthalpy (per unit mass),
, and from the definition of enthalpy (per unit mass),  . Plugging these into the above equation yields
. Plugging these into the above equation yields
 . As an example of a case where this is not the case, i.e. a case in which
. As an example of a case where this is not the case, i.e. a case in which  , consider the control volume sketched below in which part of the control surface lies along a moving wall with friction. (The top wall is moving, but the bottom wall is fixed.)
, consider the control volume sketched below in which part of the control surface lies along a moving wall with friction. (The top wall is moving, but the bottom wall is fixed.)
 , so,
, so,  .
. = 0: Recall when we talked about the momentum equation, we had a
= 0: Recall when we talked about the momentum equation, we had a  term that was hard to evaluate. Fortunately, we could either eliminate it by proper choice of C.V. or let it be the unknown. A similar thing happens in the energy equation.
We have,
term that was hard to evaluate. Fortunately, we could either eliminate it by proper choice of C.V. or let it be the unknown. A similar thing happens in the energy equation.
We have, 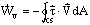

 (i.e. there is a shear stress acting on the fluid.) But,
(i.e. there is a shear stress acting on the fluid.) But,  (no slip condition at a wall!), i.e.
(no slip condition at a wall!), i.e.  .
. , but no motion
, but no motion  . Thus, the net viscous work along this wall is zero.
. Thus, the net viscous work along this wall is zero.
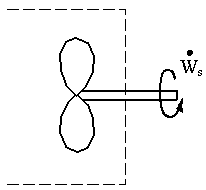
 . However, we can draw the C.V. around the whole thing! We simply include all of the viscous and pressure work terms on these blades as part of
. However, we can draw the C.V. around the whole thing! We simply include all of the viscous and pressure work terms on these blades as part of  .So here, even though
.So here, even though  is not zero along the blades themselves, we can avoid evaluating the integral since we include it in
is not zero along the blades themselves, we can avoid evaluating the integral since we include it in  , which is usually either a given or an unknown in the problem. So
, which is usually either a given or an unknown in the problem. So on our chosen C.V. (surrounding the turbine), but
on our chosen C.V. (surrounding the turbine), but  . In other words, we can lump all the viscous work terms together into one term, and call it
. In other words, we can lump all the viscous work terms together into one term, and call it  .
.

 . Therefore the viscous work term must be zero
. Therefore the viscous work term must be zero  .
.

 (by definition of the dot product). So, in this case too,
(by definition of the dot product). So, in this case too,  .
.

 .
.




 , how much heat is transferred into the compressor (in BTU/hr)? Note: We expect
, how much heat is transferred into the compressor (in BTU/hr)? Note: We expect  to be negative, since heat is given off by the compressor)]
to be negative, since heat is given off by the compressor)]
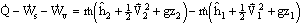
 . Also, gz1 and gz2 can be neglected because potential energy for air is generally negligible, especially in a case like this where there is a lot of heat transfer and corresponding change in enthalpy. The inlet velocity,
. Also, gz1 and gz2 can be neglected because potential energy for air is generally negligible, especially in a case like this where there is a lot of heat transfer and corresponding change in enthalpy. The inlet velocity,  can also be neglected here. With these simplifications, the energy equation becomes
can also be neglected here. With these simplifications, the energy equation becomes
 . Thus,
. Thus,  , and the heat transfer becomes
, and the heat transfer becomes  . This is the answer in variable form; all that remains is to plug in the numbers.
. This is the answer in variable form; all that remains is to plug in the numbers. 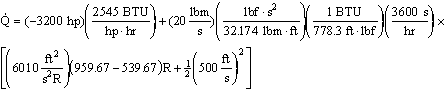
 .
.
 is negative because heat is given off by a compressor. This is a huge compressor. A typical window air conditioner can cool 5000 BTU/hr. The above answer is 100 times that!
is negative because heat is given off by a compressor. This is a huge compressor. A typical window air conditioner can cool 5000 BTU/hr. The above answer is 100 times that!
 . In the energy equation, consider the kinetic energy flux term,
. In the energy equation, consider the kinetic energy flux term,  . Because of the V3 term here, the integrand is non-linear and thus it turns out that
. Because of the V3 term here, the integrand is non-linear and thus it turns out that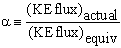
 .
. 
 , and some comments:
, and some comments:  = 1.0
= 1.0  = 2.0
= 2.0  = 1.04 - 1.11 (depends on Reynolds Number - if Reynolds number is unknown, I usually let
= 1.04 - 1.11 (depends on Reynolds Number - if Reynolds number is unknown, I usually let  = 1.06)
= 1.06)  does not affect the solution too much. But, for laminar flow,
does not affect the solution too much. But, for laminar flow,  is very important.
is very important.  in the equation.
in the equation.  . (Recall, as long as our control surface does not lie along a moving wall with friction, this viscous work term will be identically zero.)
. (Recall, as long as our control surface does not lie along a moving wall with friction, this viscous work term will be identically zero.) 
 (specific enthalpy) and
(specific enthalpy) and  (density). In addition, the elevations (z) at the inlet and outlet are known.
(density). In addition, the elevations (z) at the inlet and outlet are known.  ,
, , which will make the dimension of each term equal to length (or head, which is desired). Also, use the definition of specific enthalpy,
, which will make the dimension of each term equal to length (or head, which is desired). Also, use the definition of specific enthalpy,  . The equation becomes
. The equation becomes , or rearranging,
, or rearranging,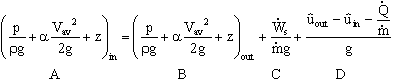
 .
.  is positive for turbines and negative for pumps. Since term C has dimensions of length, i.e. head, we can define the following positive heads for pumps and turbines:
is positive for turbines and negative for pumps. Since term C has dimensions of length, i.e. head, we can define the following positive heads for pumps and turbines: and
and 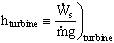
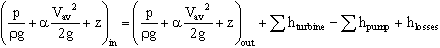 ,
,
 is the angular velocity of the rotating shaft which drives the pump. The shaft power,
is the angular velocity of the rotating shaft which drives the pump. The shaft power,  , is negative since work is being done on the control volume. Also, let T be defined as the torque on the rotating shaft. Here are some necessary definitions:
, is negative since work is being done on the control volume. Also, let T be defined as the torque on the rotating shaft. Here are some necessary definitions:  . By convention, BHP is by convention always a positive value. Note that the term "horsepower" has made its way into the literature, and is retained even if working in SI units.
. By convention, BHP is by convention always a positive value. Note that the term "horsepower" has made its way into the literature, and is retained even if working in SI units.  .
. .
.  .
. .
.  and
and  .
. and
and  .
.  , hlosses, and the elevations z0, z1, and z2. Note that hlosses represents irreversible head losses due to friction in the pipe and due to turbulent mixing and other irreversible losses in the pipe elbow and the inlet region of the pipe. At this point in our study, we do not know how to calculate these, but later on we will learn how to estimate these head losses.
, hlosses, and the elevations z0, z1, and z2. Note that hlosses represents irreversible head losses due to friction in the pipe and due to turbulent mixing and other irreversible losses in the pipe elbow and the inlet region of the pipe. At this point in our study, we do not know how to calculate these, but later on we will learn how to estimate these head losses. = constant.
= constant. where
where  , which leads to Q2 = Q1 = Q (Q is given in the problem statement).
, which leads to Q2 = Q1 = Q (Q is given in the problem statement). 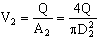
 but since
but since  . This is a direct result of our wise choice of control volume, and will reduce the complexity of the energy equation significantly.
. This is a direct result of our wise choice of control volume, and will reduce the complexity of the energy equation significantly. 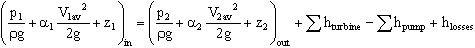
 . The head losses are known from the problem statement; solving for WHP, the energy equation thus reduces to
. The head losses are known from the problem statement; solving for WHP, the energy equation thus reduces to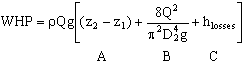
 .
. 

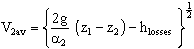
 , and V2av becomes
, and V2av becomes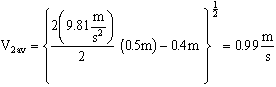
 , and V2av becomes 1.36 m/s.
, and V2av becomes 1.36 m/s.  , the answer for both laminar and turbulent flow becomes V2av = 1.40 m/s.
, the answer for both laminar and turbulent flow becomes V2av = 1.40 m/s.  should not be ignored, since it makes a big difference in the solution (here around 40%!). For turbulent flow, since
should not be ignored, since it makes a big difference in the solution (here around 40%!). For turbulent flow, since