Timothy W. Simpson,^* Andrew J. Booker,^† Dipankar Ghosh,^‡ Anthony A. Giunta,^§ Patrick N. Koch,^¶ and Ren-Jye Yang^#

Abstract
This paper summarizes the discussion at the Approximation Methods Panel that was held at the 9^th AIAA/ISSMO Symposium on Multidisciplinary Analysis & Optimization in Atlanta, GA on September 2-4, 2002. The objective in the panel was to discuss the current state-of-the-art of approximation methods and identify future research directions important to the community. The panel consisted of five representatives from industry and government: Andrew J. Booker from The Boeing Company, Dipankar Ghosh from Vanderplaats Research & Development, Anthony A. Giunta from Sandia National Laboratories, Patrick N. Koch from Engineous Software, and Ren-Jye Yang from Ford Motor Company. Each panelist was asked to (1) describe the current state-of-the-art of the approximation methods used by his company, (2) give one or two brief examples of typical uses of these methods by his company, (3) describe the current challenges in the use and adoption of approximation methods within your company, and (4) identify future research directions in approximation methods. Common themes that arose from the discussion included differentiating between Design of Experiments and Design and Analysis of Computer Experiments, visualizing experimental results and data from approximation models, capturing uncertainty with approximation methods, handling problems with large numbers of variables, and educating engineers in using approximation methods.

Keywords: approximation methods, surrogate models, response surfaces, kriging, design of experiments, analysis of variance

Author Information:
* Assistant Professor, Department of Mechanical & Nuclear Engineering, 329 Leonhard Building, Penn State University, University Park, PA 16802. Email: tws8@psu.edu. Corresponding author. Phone/fax: (814) 863-7136/4745.
† Associate Technical Fellow, Mathematics and Computing Technology Organization, The Boeing Company, Bellevue, WA 98124. Email: andrew.j.booker@pss.Boeing.com.
‡ Product Manager, Vanderplaats Research & Development, Inc. Colorado Springs, CO, 80906. Email: dg@vrand.com.
§ Optimization and Uncertainty Estimation Department, Sandia National Laboratories, Albuquerque, NM 87185. Email: patrick.koch@engineous.com.
# Senior Staff Technical Specialist, ASME Fellow, Optimization & Robustness, Safety Research & Development Department, Ford Research Laboratory, Dearborn, MI 48124. Email: ryang@ford.com.

Computer-based simulation and analysis is used extensively in engineering for a variety of tasks. Despite the steady and continuing growth of computing power and speed, the computational cost of complex high-fidelity engineering analyses and simulations maintains pace. For instance, Ford Motor Company reports that one crash simulation on a full passenger car takes 36-160 hours.¹ The high computational expense of such analyses limits, or often prohibits, the use of such codes in engineering design and multidisciplinary design optimization (MDO). Consequently, approximation methods such as design of experiments and response surface models are commonly used in engineering design to minimize the computational expense of running such analyses and simulations. The basic approach is to construct a simplified mathematical approximation of the computationally expensive simulation and analysis code, which is then used in place of the original code to facilitate multidisciplinary design optimization, design space exploration, reliability analysis, etc. Since the approximation model acts as a surrogate for the original code, it is often referred to as a surrogate model, surrogate approximation, approximation model, or metamodel (i.e., a "model of a model"²). A variety of approximation models exist (e.g., polynomial response surfaces, kriging models, radial basis functions, neural networks, multivariate adaptive regression splines), and recent reviews and comparisons of many of these approximation model types can be found in Refs. 3-9.

To gain a better understanding of how approximation methods are currently viewed and being used by industry and government agencies, a panel discussion on Approximation Methods was held at the 9^th AIAA/ISSMO Symposium on Multidisciplinary Analysis & Optimization (MA&O) in Atlanta, GA on September 2-4, 2002. The objective in the panel was to discuss the current state-of-the-art of approximation methods and identify future research directions important to the community. The panel consisted of five representatives from industry and government: (1) Andrew J. Booker from The Boeing Company, (2) Dipankar Ghosh from Vanderplaats Research & Development, (3) Anthony A. Giunta from Sandia National Laboratories, (4) Patrick N. Koch from Engineous Software, and (5) Ren-Jye Yang from Ford Motor Company. Each panelist was asked to (1) describe the current state-of-the-art of the approximation methods used by his company, (2) give one or two brief examples of typical uses of these methods by his company, (3) describe the current challenges in the use and adoption of approximation methods within your company, and (4) identify future research directions in approximation methods.

The remainder of this paper summarizes the discussion that occurred at the panel and is intended to serve as a record for the approximation methods community at large who were unable to attend. Section II contains a brief overview of the example applications discussed by the panelists along with a list of the approximation software presented during the panel. Common themes that arose from the discussion included differentiating between Design of Experiments and Design and Analysis of Computer Experiments (Section III), visualizing experimental results and data from approximation models (Section IV), capturing uncertainty with approximation methods (Section V), and handling problems with large numbers of variables (Section VI). A brief summary of the questions that followed the panelists’ opening remarks are discussed as part of the closing remarks in Section VII along with future challenges such as educating engineers in using approximation methods.

A variety of applications were discussed by the panelists, indicating the wide variety of uses for approximation methods in engineering design and MDO. These applications ranged from space station power systems, to fluid flow problems and oil tanker design, to structural design and automotive crashworthiness. A brief overview of each example follows.

Booker described a Design of Experiments approach that was used to verify the performance of large DC power systems for a space station.^10-11 Up to 30 input loads could be switched ON/OFF, and Design of Experiments was used to analyze the performance of the system and determine operating conditions to achieve a desired phase margin. Since each load could be switched either ON or OFF, a 2-level fractional factorial was used to analyze the system, and analysis of variance (ANOVA) was used to estimate main effects.

An aircraft jet engine inlet design problem involving 11 geometry parameters used a 12-pt Plackett-Burman design¹² to achieve an accurate approximation to maximize the air flow rate on the inlet surface.¹³ Initially, the turnaround time to obtain response values was two weeks. The engineers were able to reduce the turnaround time (eventually to one day) by automating the set-up for analysis. The design was subsequently successively augmented by "folding over" the design to resolve interactions and adding a center point and star points to estimate quadratic effects. The benefit of the particular experimental design approach on this problem was the ability to sequentially augment the design as turnaround time was reduced.

A fluid flow example involving the design of a cooling system¹⁴ was also discussed during the panel, see Figure 1. The example consisted of 12 design variables, 10 constraints, and one objective function; feasibility and convergence were achieved in 11 iterations, requiring only 24 calls of Fluent, a computationally expensive fluid flow analysis package.

Figure 1. Visualization of Fluid Flow through Cooling System Using Fluent

An oil tanker conceptual design problem was used to compare the accuracy of a single global approximation model against two disciplinary approximation models—one for the tanker’s hydrodynamic analyses and one for the tanker’s structural analyses—that provided parameters for cost estimation.¹⁵ Both approximation models yielded an improvement in the objective function (i.e., return on investment), but the two disciplinary approximation models required fewer expensive analyses than the global approximation model did.

Approximation methods for structural analysis and automotive crashworthiness were discussed by several panelists. An automobile design example involving the use of topology optimization to improve the structural rigidity of the body was described.¹⁶ Vehicle safety analysis is a complex and computationally expensive process, and researchers at Ford are investigating the accuracy of different approximation types for automotive crashworthiness studies.^1,17-18 Yang, et al.¹⁸ stress the importance of uniform sampling when only small sets of sample points are available due the computational expense of running crash simulations such as that shown in Figure 2a. A probabilistic formulation for addressing uncertainty in automotive design was also presented to help identify designs that are robust to the multiple crash scenarios (see Figure 2b) that are considered during automotive crashworthiness studies.^19-20

Figure 2. Automotive Crashworthiness¹⁸

In addition to these examples, several software packages for building, constructing, validating, and optimizing approximation models were also discussed during the panel. To avoid commercialism and bias, the reader is referred to the following references and URLs to learn more about the capabilities of the approximation software packages discussed by the panelists:

• DAKOTA: Ref. 21 and http://endo.sandia.gov/DAKOTA.
• iSIGHT: Ref. 22 and http://www.engineous.com/products.htm.
• VisualDOC: Ref. 23 and http://www.vrand.com/visualdoc3info.htm.

In addition to these packages, Design Explorer is being developed at The Boeing Company to provide similar capabilities.²⁴

As mentioned previously, several common themes arose from the panel discussion, including the need to differentiate between traditional Design of Experiments (DOE) and response surface (RS) modeling and Design and Analysis of Computer Experiments (DACE), which often employs kriging models, see Figure 3. In the "classical" design and analysis of physical experiments, random variation is accounted for by spreading the sample points out in the design space and by taking multiple data points (replicates) as shown in the figure. This is an important distinction between physical experiments, which have random error, and computer experiments, which are often deterministic (i.e., the same output is obtained each time the same input is given), that was made frequently during the panel. Sacks, et al.²⁵ state that the "classical" notions of blocking, replication, and randomization are irrelevant when it comes to deterministic computer experiments; thus, sample points should be chosen to fill the design space. Space filling experimental designs include latin hypercube designs,²⁶ orthogonal arrays,^27-28 uniform designs,^29-30 Hammersley sampling sequences,³¹ and minimax and maximin designs³² to name a few. A recent comparison of several space filling designs can be found in Ref. 3

Figure 3. Comparison of DOE/RS and DACE/Kriging

Once sample data has been gathered, response surface modeling typically employs least squares regression to fit a polynomial model, typically first- or second-order, to the sampled data. Additional details on least squares regression can be found in a number of texts.^33,35-36 Kriging models are constructed using maximum likelihood estimation (see, e.g., Ref. 25, 34, 37-40) and typically interpolate the data, providing an exact fit of the sampled data. Non-interpolative kriging models that "smooth" noisy data can also be developed.^41-43

Once the approximation model is constructed, it must be validated in order to ensure that it is sufficiently accurate to use as a surrogate for the original code. Validation of response surface models is typically based on: (a) testing statistical hypothesis (t-tests and F-statistics) derived from error estimates of the variability in the data, (b) plotting and checking the residuals, and (c) computing R², the ratio of the model sum of squares to the total sum of squares, and R²_adj, which is R² adjusted for the number of parameters in the model.³³ Jin, et al.⁵ discuss multiple performance metrics for comparing approximation models based on accuracy, efficiency, robustness, model transparency, and simplicity; Yang added that Gearhart and Wang⁴⁴ discuss metrics for comparing response surfaces models of different order to identify the "best" model.

Sacks, et al.²⁵ and Welch, et al.⁴⁵ state that statistical testing is inappropriate when it comes to deterministic computer experiments which lack random error; therefore, cross-validation and integrated mean square error (MSE) are often employed to assess the accuracy of a kriging model. A simplified procedure for leave-one-out cross validation of kriging models is presented by Mitchell and Morris,⁴⁶ but recent studies by Meckesheimer, et al.⁴⁷ found that leave-one-out cross validation does not work well for validating kriging models. Leave-one-out cross validation often under-estimates the true root mean square error in a kriging model, and they suggest using the more general leave-k-out cross validation for kriging models with k=0.1n or n^1/2 where n is the number of sample points used to fit the model.

The importance of visualization was stressed by nearly every panelist. First, visualization is useful for examining the experimental results themselves and can be used to detect potential outliers in the data. Booker described a case were an errant run of a simulation code yielded a response about 10⁶ orders of magnitude greater than the other responses, which caused the resulting kriging approximation to fit poorly. The engineers had not noticed the outlier when they examined the experimental data file, but it showed up immediately when the design space was plotted in 3D.

In addition to viewing the experimental results, approximation models also provide a useful surrogate for visualizing the entire design space. Koch gave the example shown in Figure 4 of three approximation models fit to the same set of sample data—all three can be used to view the design space, but which is the most accurate? Based on the sample data, this is found to be a highly non-linear design space that cannot be accurately represented by a second-order RS model as seen in Figure 4a. Obviously a higher-order polynomial response surface model can be constructed, a fourth-order RS model is shown in Figure 4b, but this often requires more sample data than is readily available. The best fit of the sample data is provided by the kriging model shown in Figure 4c, which has sufficient flexibility to fit the highly non-linear design space. An example of a graphical comparison of response surface and kriging models for the design of an aerospike rocket nozzle can be found in Ref. 40.

Figure 4. Graphical Comparison of Response Surface and Kriging Model

Visualization also plays an important role in optimization. Ghosh stressed the importance of viewing the history of the objective function during optimization to monitor system performance. Koch advocated using the approximation model to view design variable values in real-time as they changed during optimization. Booker stated that visualization is helpful in understanding why a point is optimum and how it might be improved if constraints are changed or relaxed.

Panelists emphasized that these visualization capabilities do not have to be very sophisticated. Booker uses bar charts and pie charts to display functional ANOVA results to help identify important main effects and interactions based on the sample data.^11,34,48 Depending on the type of experimental design, the functional ANOVA can be computed directly, if using an orthogonal array of strength of strength 3 or higher²⁸, or can be estimated from the approximation model itself. Booker showed results from a sinusoidal test function proposed by Giunta and Watson³⁹ to demonstrate the useful information that could be gained through functional ANOVA but with some caution when using approximate models to estimate the ANOVA.⁴⁹

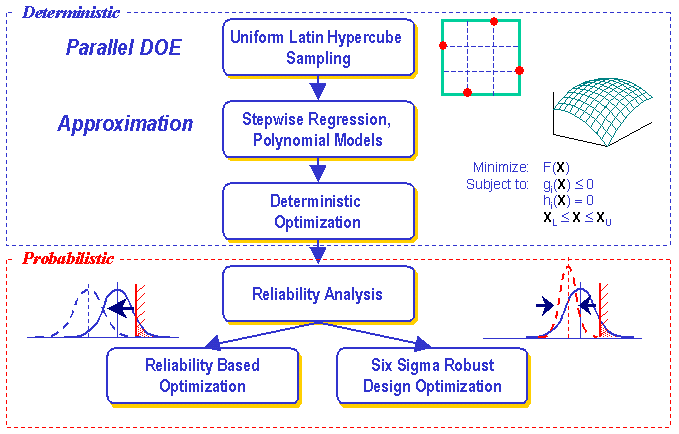
Approximation methods are becoming popular tools for modeling uncertainty and reducing the computational expense of probabilistic analysis during probabilistic design optimization. Koch stated that a variety of probabilistic methods have been developed to model and assess the effects of known uncertainties by converting deterministic problem formulations into probabilistic formulations, but until recently the computational expense of probabilistic analysis of a given design often precluded its application to real engineering design problems, and probabilistic optimization has thus been considered impractical, particularly for complex multidisciplinary problems. He stated that approximation methods are finding new uses in reducing the computational expensive of probabilistic analysis to make probabilistic optimization more tractable. For instance, approximation models are being used at Ford to incorporate uncertainty into automotive crashworthiness studies.^19-20 Koch also outlined a procedure for using approximation methods to facilitate reliability analysis and robust design optimization, see Figure 5. As an example, the oil tanker example described in Section II was used to compare the performance of response surface and kriging approximations for six sigma based probabilistic design optimization in Ref. 50.

Figure 5. Probabilistic Analysis Using Approximation Methods⁵¹

Giunta used the plot in Figure 6 to illustrate the differences between a global non-robust optimum and a local robust optimum for a computational shock physics application.⁵² The application uses a large finite element code to simulate the shock physics involved with imploding an inertial confinement fusion capsule that is subject to manufacturing variation. Given manufacturing variation in the radius of the outer layer of plastic ablator material that surrounds the capsule, he stated that was more important to find robust, "flat" regions in the design space that are insensitive to these variations than it was to find the global optimum.

Figure 6. Robust Design in Shock Physics⁵³

Giunta presented the following formulation for simulation-based optimization under uncertainty:

where S(x,u) are statistical metrics (e.g., means, standard deviations, failure probabilities, etc.) and W and A are weighting vectors/matrices. Approximation models are employed for f(x), g(x), and S(x,u) to reduce the computational expense of these analyses. Detailed results for the computational shock physics example shown in Figure 6 can be found in Ref. 53. Giunta also mentioned that approximation models are useful for reducing the numerical noise that might occur in the output responses, citing his earlier work wherein response surface models helped smooth numerical noise in an aerodynamic analysis example.⁵⁴ While optimization and uncertainty quantification are becoming more important, they are still not viewed as critical path items at Sandia; he said the focus is still on "getting the physics right."

Often referred to as the "curse of dimensionality,"^55-57 a constant challenge in building accurate approximation models is handling problems with large numbers of variables: the more design variables you have, the more samples you need to build an accurate metamodel. This becomes increasingly important when modeling uncertainty because the design (input) variables and the uncertain (noise) variables must be captured in the model, thereby increasing the dimensionality of the design space even more.

Screening experiments are often employed to reduce the set of factors to those that are most important to the response(s) being investigated. Statistical experimentation is used to define the appropriate design analyses that must be run to evaluate the desired effects of the factors. Often two level fractional factorial designs⁵⁸ or Plackett-Burman¹² designs are used for screening, and only main (linear) effects of each factor are investigated.

Among the earliest such work, Box and Draper⁵⁹ proposed a method to gradually refine a response surface model to better capture the real function by "screening" out unimportant variables. Ghosh discussed the use of intermediate design variables to reduce the dimensionality of the design space; a topology optimization example of an automobile body to improve structural rigidity was given as an example.¹⁶ The variable-complexity response surface modeling method uses analyses of varying fidelity to reduce the design space to the region of interest.^60-62 A procedure for screening unimportant variables is offered by Welch, et al.,⁶³ which uses a kriging-based approximation methodology to identify important variables, detect curvature and interactions, and produce a useful approximation model for two 20 variable problems using only 30-50 runs of the computer code. Booker noted, however, that the interaction between screening methods and optimization still needs to be investigated further. For instance, variables that might not be important during initial experimentation may become important in the later stages of the optimization such that the variables that were initially "screened out" need to be added back into the model.

Problems involving mixed discrete/continuous variables were also mentioned as one of the challenges facing the design of experiments for building approximation models. Booker emphasized that the judicious selection of the experimental design is needed when factors with discrete levels are considered. For instance, the design variables for the power system examples^10-11 mentioned in Section II had ON/OFF levels, mandating the use of an experimental design with two levels. Orthogonal arrays with discrete level choices are also available for problems with two or more discrete levels.²⁸ In general though, problems with both continuous and discrete variables require special consideration and have thus far been solved largely on a problem-by-problem basis.

The discussion that followed the presentations by the panelists revolved primarily around the research topics outlined in the previous sections. Two additional topics that continued to surface during the discussion involved using gradient information in approximation models and sequential methods for model fitting and building. Yang stated that gradient information was usually not readily available in their crashworthiness models; therefore, he did not advocate the use of gradient-enhanced approximations because obtaining gradient information added computational expensive. Booker and Giunta agreed that if the information was readily available, or could be easily obtained through procedures such as automatic differentiation,⁶⁴ then it should be used to improve the accuracy of the approximation model; Booker recommended a paper by Morris, et al.⁶⁵ that offered a method for using gradient information in kriging models and a paper by Koehler⁶⁶ that discusses the use of gradient information in kriging models and its usefulness for estimating transmitted variation. Methods for using gradient information to enhance approximation models were also being developed by several members of the audience.^67-69

Sequential and adaptive approximation methods were also being developed by several members of the audience.^70-74 A sequential method combining response surface models and kriging models was also mentioned,⁷⁵ which used "inherited" sample points in latin hypercube designs as new samples were taken.⁷⁶ The merits of sequentially sampling the design space⁷⁷ to improve the accuracy of the approximation model in one or more regions of interest were also discussed. The work by Osio and Amon⁷⁸ was cited for their multi-stage sampling procedure for building kriging models.

Kriging models for approximation and global optimization were another big topic of discussion. In fact, more papers involving kriging-based approximation models appeared at this MA&O Symposium than at the past symposiums combined. Global optimization procedures using kriging models were discussed,^24,79-80 and a procedure for calibrating a kriging model during optimization that avoided problems with an ill-conditioned correlation matrix was discussed by Booker,⁸¹ see Figure 7. Procedures for updating the theta parameters in a kriging model during continuous experimentation are investigated in Ref. 82.

Figure 7. Kriging Model Calibration during Optimization⁸¹

In addition to outlining research directions for advancing approximation methods themselves, panelists also charged the academic community with helping to educate engineers in how to use them. Ghosh emphasized that engineers should gain some basic exposure to approximation methods and their uses. He said that a strong theoretical background was not necessary, but it was important to know how to formulate a problem and interpret results to identify when problems occur. Koch echoed his comments, stating that a basic level of understanding is needed to build, validate, exercise approximation models even though the majority of these processes are automated by software packages. A similar philosophy is used in academia when teaching finite element methods prior to using a finite element software package.

Giunta also stated that many engineers and analysts do not have sufficient background in applied math (i.e., optimization) and statistics to understand approximation methods and how they are used. They are often unfamiliar with the statistical terms and concepts and are overwhelmed by the many choices available for the experimental design (e.g., central composite designs, latin hypercubes, uniform designs, orthogonal arrays) and the approximation model (e.g., kriging, response surfaces, neural net, etc.). He closed in saying that good graphical user interfaces can help mitigate this but considerable "hand-holding" is needed in the meantime. Booker made similar comments, stating that it is helpful to know what an engineer plans to do with the results (e.g., identify main effects, screen variables, use the approximation for optimization) since that often dictates the approach and tools employed in the study.

References

¹Gu, L., "A Comparison of Polynomial Based Regression Models in Vehicle Safety Analysis," ASME Design Engineering Technical Conferences - Design Automation Conference (DAC) (Diaz, A., ed.), Pittsburgh, PA, ASME, September 9-12, 2001, Paper No. DETC2001/DAC-21063.

²Kleijnen, J. P. C., "A Comment on Blanning's Metamodel for Sensitivity Analysis: The Regression Metamodel in Simulation," Interfaces, Vol. 5, No. 1, 1975, pp. 21-23.

³Simpson, T. W., Lin, D. K. J. and Chen, W., "Sampling Strategies for Computer Experiments: Design and Analysis," International Journal of Reliability and Applications, Vol. 2, No. 3, 2001, pp. 209-240.

⁴Simpson, T. W., Peplinski, J., Koch, P. N. and Allen, J. K., "Metamodels for Computer-Based Engineering Design: Survey and Recommendations," Engineering with Computers, Vol. 17, No. 2, 2001, pp. 129-150.

⁵Jin, R., Chen, W. and Simpson, T. W., "Comparative Studies of Metamodeling Techniques under Multiple Modeling Criteria," Journal of Structural and Multidisciplinary Optimization, Vol. 23, No. 1, 2001, pp. 1-13.

⁶Sobieszczanski-Sobieski, J. and Haftka, R. T., "Multidisciplinary Aerospace Design Optimization: Survey of Recent Developments," Structural Optimization, Vol. 14, No. 1, 1997, pp. 1-23.

⁷Haftka, R., Scott, E. P. and Cruz, J. R., "Optimization and Experiments: A Survey," Applied Mechanics Review, Vol. 51, No. 7, 1998, pp. 435-448.

⁸Barthelemy, J.-F. M. and Haftka, R. T., "Approximation Concepts for Optimum Structural Design - A Review," Structural Optimization, Vol. 5, 1993, pp. 129-144.

⁹Barton, R. R., "Simulation Metamodels," Proceedings of the 1998 Winter Simulation Conference (WSC'98) (Medeiros, D. J., Watson, E. F., et al., eds.), Washington, DC, IEEE, December 13-16, 1998, pp. 167-174.

¹⁰Karimi, K. J., Booker, A. J. and Mong, A., "Modeling, Simulation and Verification of Large DC Power Electronics Systems," Proceedings of the 27th Annual IEEE Power Electronics Specialists Conference, Baveno, Italy, IEEE, Vol. 2, June 23-27, 1996, pp. 1731-1738.

¹¹Karimi, K. J., Booker, A. J., Manners, B. and Mong, A., "Verification of Space Station Secondary Power System Stability Using Design of Experiment," Proceedings of the 32nd Intersociety Energy Conversion Engineering Conference, IEEE, Vol. 1, July 27-August 1, 1997, pp. 526-531.

¹²Plackett, R. L. and Burman, J. P., "The Design of Optimum Multifactorial Experiments," Biometrika, Vol. 33, No. 4, 1946, pp. 305-325.

¹³Mason, J. G., Farquhar, B. W., Booker, A. J. and Moody, R. J., "Inlet Design Using a Blend of Experimental and Computational Techniques," Proceedings of the 18th Congress of ICAS, Vol. 1, 1992, ICAS-92-3.3.1.

¹⁴Quinn, G., "Cooling System Design Using Approximation Methods," Working Paper, Vanderplaats Research & Development, Inc., Colorado Springs, CO, 2002.

¹⁵Golovidov, O., Kodiyalam, S., Marineau, P., Wang, L. and Rohl, P., "A Flexible, Object-based Implementation of Approximation Models in an MDO Framework," Design Optimization: International Journal for Product & Process Improvement, Vol. 1, No. 4, 1999, pp. 388-404.

¹⁶Leiva, J. P., Wang, L., S., R. and Watson, B., "Automobile Design Using the GENESIS Structural Optimization Program," Nafems Seminar: Advances in Optimization Technologies for Product Design, Chicago, IL, October 22-23, 2001.

¹⁷Yang, R. J., Gu, L., Liaw, L., Gearhart, C., Tho, C. H., Liu, X. and Wang, B. P., "Approximations for Safety Optimization of Large Systems," ASME 2000 Design Engineering Technical Conferences - Design Automation Conference (Renaud, J. E., ed.), Baltimore, MD, ASME, September 10-13, 2000, Paper No. DETC-2000/DAC-14245.

¹⁸Yang, R. J., Wang, N., Tho, C. H. and Bobineau, J. P., "Metamodeling Development for Vehicle Frontal Impact Simulation," ASME Design Engineering Technical Conferences - Design Automation Conference (DAC) (Diaz, A., ed.), Pittsburgh, PA, ASME, September 9-12, 2001, Paper No. DETC2001/DAC-21012.

¹⁹Koch, P. N., Yang, R.-J. and Gu, L., "Design for Six Sigma Through Robust Optimization," Structural and Multidiscipilnary Optimization, 2002, in press.

²⁰Koch, P. N. and Gu, L., 2001, "Addressing Uncertainty using the iSIGHT Probabilistic Design Environment," First Annual Probabilistic Methods Conference, Newport Beach, CA, June 18-19, 2001.

²¹Eldred, M. S., Giunta, A. A., van Bloemen Waanders, B. G., Wojtkiewicz, S. F., Jr., Hart, W. E. and Alleva, M. P., "DAKOTA, A Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis. Version 3.0 Users Manual," Sandia Technical Report SAND2001-3796, Sandia National Laboratories, Albuquerque, NM, 2002.

²²Koch, P. N., Evans, J. P. and Powell, D., "Interdigitation for Effective Design Space Exploration using iSIGHT," Structural and Multidiscipilnary Optimization, Vol. 23, No. 2, 2002, pp. 111-126.

²³Balabanov, V., Charpentier, C., Ghosh, D. K., Quinn, G., Vanderplaats, G. and Venter, G., "VisualDOC: A Software System for General Purpose Integration and Design Optimization," 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, AIAA, September 4-6, 2002, AIAA-2002-5513.

²⁴Booker, A. J., Dennis, J. E., Jr., Frank, P. D., Serafini, D. B., Torczon, V. and Trosset, M. W., "A Rigorous Framework for Optimization of Expensive Functions by Surrogates," Structural Optimization, Vol. 17, No. 1, 1999, pp. 1-13.

²⁵Sacks, J., Welch, W. J., Mitchell, T. J. and Wynn, H. P., "Design and Analysis of Computer Experiments," Statistical Science, Vol. 4, No. 4, 1989, pp. 409-435.

²⁶McKay, M. D., Beckman, R. J. and Conover, W. J., "A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code," Technometrics, Vol. 21, No. 2, 1979, pp. 239-245.

²⁷Hedayat, A. S., Sloane, N. J. A. and Stufken, J., Orthogonal Arrays: Theory and Applications, Springer, New York, 1999.

²⁸Owen, A. B., "Orthogonal Arrays for Computer Experiments, Integration and Visualization," Statistica Sinica, Vol. 2, 1992, pp. 439-452.

²⁹Fang, K.-T. and Wang, Y., Number-theoretic Methods in Statistics, Chapman & Hall, New York, 1994.

³⁰Fang, K.-T., Lin, D. K. J., Winker, P. and Zhang, Y., "Uniform Design: Theory and Application," Technometrics, Vol. 42, 2000, pp. 237-248.

³¹Kalagnanam, J. R. and Diwekar, U. M., "An Efficient Sampling Technique for Off-Line Quality Control," Technometrics, Vol. 39, No. 3, 1997, pp. 308-319.

³²Johnson, M. E., Moore, L. M. and Ylvisaker, D., "Minimax and Maximin Distance Designs," Journal of Statistical Planning and Inference, Vol. 26, No. 2, 1990, pp. 131-148.

³³Myers, R. H. and Montgomery, D. C., Response Surface Methodology: Process and Product Optimization Using Designed Experiments, John Wiley & Sons, New York, 1995.

³⁴Booker, A. J., "Design and Analysis of Computer Experiments," 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis & Optimization, St. Louis, MO, AIAA, Vol. 1, September 2-4, 1998, pp. 118-128.

³⁵Box, G. E. P. and Draper, N. R., Empirical Model Building and Response Surfaces, John Wiley & Sons, New York, 1987.

³⁶Box, G. E. P., Hunter, W. G. and Hunter, J. S., Statistics for Experimenters: An Introduction to Design, Data Analysis, and Model Building, John Wiley & Sons, New York, 1978.

³⁷Currin, C., Mitchell, T., Morris, M. and Ylvisaker, D., "Bayesian Prediction of Deterministic Functions, With Applications to the Design and Analysis of Computer Experiments," Journal of the American Statistical Association, Vol. 86, No. 416, 1991, pp. 953-963.

³⁸Koehler, J. R. and Owen, A. B., "Computer Experiments," Handbook of Statistics (Ghosh, S. and Rao, C. R., eds.), Elsevier Science, New York, 1996, pp. 261-308.

³⁹Giunta, A. and Watson, L. T., "A Comparison of Approximation Modeling Techniques: Polynomial Versus Interpolating Models," 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis & Optimization, St. Louis, MO, AIAA, Vol. 1, September 2-4, 1998, pp. 392-404.

⁴⁰Simpson, T. W., Mauery, T. M., Korte, J. J. and Mistree, F., "Kriging Metamodels for Global Approximation in Simulation-Based Multidisciplinary Design Optimization," AIAA Journal, Vol. 39, No. 12, 2001, pp. 2233-2241.

⁴¹Cressie, N., "Spatial Prediction and Ordinary Kriging," Mathematical Geology, Vol. 20, No. 4, 1988, pp. 405-421.

⁴²Montès, P., "Smoothing Noisy Data by Kriging with Nugget Effects," Wavelets, Images and Surface Fitting (Laurent, P. J., Le Méhauté, A., et al., eds.), A.K. Peters, Wellesley, MA, 1994, pp. 371-378.

⁴³Kleijnen, J. P. C. and Van Beers, W., "Kriging for Interpolation in Random Simulation," Journal of the Operational Research Society, 2002, in press.

⁴⁴Gearhart, C. and Wang, B. P., "Bayesian Metrics for Comparing Response Surface Models for Data with Uncertainty," Structural and Multidisciplinary Optimization, Vol. 22, No. 3, 2001, pp. 198-207.

⁴⁵Welch, W. J., Yu, T.-K., Kang, S. M. and Sacks, J., "Computer Experiments for Quality Control by Parameter Design," Journal of Quality Technology, Vol. 22, No. 1, 1990, pp. 15-22.

⁴⁶Mitchell, T. J. and Morris, M. D., "Bayesian Design and Analysis of Computer Experiments: Two Examples," Statistica Sinica, Vol. 2, 1992, pp. 359-379.

⁴⁷Meckesheimer, M., Barton, R. R., Simpson, T. W. and Booker, A., "Computationally Inexpensive Metamodel Assessment Strategies," AIAA Journal, Vol. 40, No. 10, 2002, pp. 2053-2060.

⁴⁸Booker, A., "Examples of Surrogate Modeling of Computer Simulations," ISSMO/NASA First Internet Conference on Approximations and Fast Reanalysis in Engineering Optimization, 2000.

⁴⁹Booker, A., "Using Metamodels for Engineering Design," INFORMS Seattle Fall 1998 Meeting, Seattle, WA, INFORMS, October 25-28, 1998.

⁵⁰Koch, P. N., Golovidov, O., Wujek, B. A. and Simpson, T. W., "Facilitating Probabilistic Multidisciplinary Design Optimization through Advanced Approximation Methods," 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, AIAA, September 4-6, 2002, AIAA-2002-5415.

⁵¹Koch, P. N., "Probabilistic Design: Optimizing for Six Sigma Quality," 43rd AIAA/ASME/ASCE/AHS Structures, Structural Dynamics, and Materials Conference, 4th AIAA Non-Deterministic Approaches Forum, Denver, CO, AIAA, 2002, AIAA-2002-1471.

⁵²Giunta, A. A., Eldred, M. S., Trucano, T. G. and Wojtkiewicz, S. F., Jr., "Optimization Under Uncertainty Methods for Computational Shock Physics Applications," 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, AIAA, April 22-25, 2002, AIAA-2002-1642.

⁵³Eldred, M. S., Giunta, A. A., Wojtkiewicz, S. F., Jr. and Trucano, T. G., "Formulations for Surrogate-Based Optimization Under Uncertainty," 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, AIAA, September 4-6, 2002, AIAA-2002-5585.

⁵⁴Giunta, A. A., Dudley, J. M., Narducci, R., Grossman, B., Haftka, R. T., Mason, W. H. and Watson, L. T., "Noisy Aerodynamic Response and Smooth Approximations in HSCT Design," 5th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Panama City, FL, AIAA, Vol. 2, September 7-9, 1994, pp. 1117-1128.

⁵⁵Balabanov, V., Kaufman, M., Knill, D. L., Golovidov, O., Giunta, A. A., Haftka, R. T., Grossman, B., Mason, W. H. and Watson, L. T., "Dependence of Optimal Structural Weight on Aerodynamic Shape for a High Speed Civil Transport," 6th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Bellevue, WA, AIAA, Vol. 1, September 4-6, 1996, pp. 599-612.

⁵⁶Koch, P. N., Mavris, D. and Mistree, F., "Multi-Level, Partitioned Response Surfaces for Modeling Complex Systems," 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis & Optimization, St. Louis, MO, AIAA, Vol. 3, September 2-4, 1998, pp. 1954-1968.

⁵⁷Koch, P. N., Simpson, T. W., Allen, J. K. and Mistree, F., "Statistical Approximations for Multidisciplinary Optimization: The Problem of Size," Special Multidisciplinary Design Optimization Issue of Journal of Aircraft, Vol. 36, No. 1, 1999, pp. 275-286.

⁵⁸Montgomery, D. C., Design and Analysis of Experiments, Fourth Edition, John Wiley & Sons, New York, 1997.

⁵⁹Box, G. E. P. and Draper, N. R., Evolutionary Operation: A Statistical Method for Process Management, John Wiley & Sons, Inc., New York, 1969.

⁶⁰Balabanov, V. O., Giunta, A. A., Golovidov, O., Grossman, B., Mason, W. H. and Watson, L. T., "Reasonable Design Space Approach to Response Surface Approximation," Journal of Aircraft, Vol. 36, No. 1, 1999, pp. 308-315.

⁶¹Giunta, A. A., Balabanov, V., Kaufmann, M., Burgee, S., Grossman, B., Haftka, R. T., Mason, W. H. and Watson, L. T., "Variable-Complexity Response Surface Design of an HSCT Configuration," Multidisciplinary Design Optimization: State of the Art - Proceedings of the ICASE/NASA Langley Workshop on Multidisciplinary Design Optimization (Alexandrov, N. M. and Hussaini, M. Y., eds.), Hampton, VA, SIAM, March 13-16, 1996, pp. 348-367.

⁶²Venter, G., Haftka, R. T. and Starnes, J. H., Jr., "Construction of Response Surface Approximations for Design Optimization," AIAA Journal, Vol. 36, No. 12, 1998, pp. 2242-2249.

⁶³Welch, W. J., Buck, R. J., Sacks, J., Wynn, H. P., Mitchell, T. J. and Morris, M. D., "Screening, Predicting, and Computer Experiments," Technometrics, Vol. 34, No. 1, 1992, pp. 15-25.

⁶⁴Su, J. and Renaud, J. E., "Automatic Differentiation in Robust Optimization," AIAA Journal, Vol. 35, No. 6, 1997, pp. 1072-1079.

⁶⁵Morris, M. D., Mitchell, T. J. and Ylvisaker, D., "Bayesian Design and Analysis of Computer Experiments: Use of Derivatives in Surface Prediction," Technometrics, Vol. 35, No. 3, 1993, pp. 243-255.

⁶⁶Koehler, J. R., "Estimating the Response, Derivatives, and Transmitted Variance Using Computer Experiments," Mathematics Department, Working Paper, Univeristy of Colorado at Denver, Denver, CO, 1997.

⁶⁷Liu, W. and Batill, S., "Gradient-enhanced Neural Network Response Surface Approximations," 8th AIAA/USAF/NASA/ISSMO Symposium on Multidsciplinary Analysis & Optimization, Long Beach, CA, AIAA, September 6-8, 2000, AIAA-2000-4923.

⁶⁸Liu, W. and Batill, S. M., "Gradient-Enhanced Response Surface Approximations Using Kriging Models," 9th AIAA/ISSMO Symposium and Exhibit on Multidisciplinary Analysis and Optimization, Atlanta, GA, AIAA, September 4-6, 2002, AIAA-2002-5456.

⁶⁹van Keulen, F. and Vervenne, K., "Gradient-Enhanced Response Surface Building," 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, AIAA, September 4-6, 2002, AIAA-2002-5455.

⁷⁰Pérez, V. M., Renaud, J. E. and Watson, L. T., "Interior Point Sequential Approximate Optimization Methodology," 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis & Optimization, Atlanta, GA, AIAA, September 4-6, 2002, AIAA-2002-5505.

⁷¹Pérez, V. M., Renaud, J. E. and Watson, L. T., "Adaptive Experimental Design for Construction of Response Surface Approximations," AIAA Journal, 2002, in press.

⁷²Pérez, V. M., Renaud, J. E. and Watson, L. T., "Reduced Sampling for Construction of Quadratic Response Surface Approximations Using Adaptive Experimental Design," 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, AIAA, April 22-25, 2002, AIAA-2002-1587.

⁷³Pérez, V. M., Renaud, J. E. and Watson, L. T., "Adaptive Experimental Design for Construction of Response Surface Approximations," 42nd AIAA/ASME/ASC/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Seattle, WA, AIAA, Vol. 5, April 16-19, 2001, pp. 3221-3232.

⁷⁴Rodríguez, J. F., Pérez, V. M., Padmanabhan, D. and Renaud, J. E., "Sequential Approximate Optimization Using Variable Fidelity Response Surface Approximations," Structural and Multidisciplinary Optimization, Vol. 22, No. 1, 2001, pp. 24-34.

⁷⁵Wang, G. G. and Simpson, T. W., "Fuzzy Clustering Based Hierarchical Metamodeling for Design Optimization," 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, AIAA, September 4-6, 2002, AIAA-2002-5574.

⁷⁶Wang, G., "Adaptive Response Surface Method Using Inherited Latin Hypercube Designs," ASME Journal of Mechanical Design, 2002, in press.

⁷⁷Farhang-Mehr, A. and Azarm, S., "A Sequential Information-Theoretic Approach to Design of Computer Experiments," 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, AIAA, September 4-6, 2002, AIAA-2002-5571.

⁷⁸Osio, I. G. and Amon, C. H., "An Engineering Design Methodology with Multistage Bayesian Surrogates and Optimal Sampling," Research in Engineering Design, Vol. 8, No. 4, 1996, pp. 189-206.

⁷⁹Sasena, M., Papalambros, P. Y. and Goovaerts, P., "Global Optimization of Problems with Disconnecte Feasible Regions via Surrogate Modeling," 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, AIAA, September 4-6, 2002, AIAA-2002-5573.

⁸⁰Audet, C., Booker, A. J., Dennis, J. E., Jr, Frank, P. D. and Moore, D., "A Surrogate-Model-Based Method for Constrained Optimization," 8th AIAA/NASA/USAF/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Long Beach, CA, AIAA, September 6-8, 2000, AIAA-2000-4891.

⁸¹Booker, A., "Well-Conditioned Kriging Models for Optimization of Computer Simulations," Technical Document Series, M&CT-TECH-002, Phantom Works, Mathematics and Computing Technology, The Boeing Company, Seattle, WA, 2000.

⁸²Martin, J. D. and Simpson, T. W., "Adaptive Metamodeling for Undersea Vehicle Design Optimization," 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, AIAA, September 4-6, 2002, AIAA-2002-5631.